Relación y Función
Producto Cartesiano
El producto cartesiano de dos
conjuntos A y B, denotado A × B, es el conjunto de todos los posibles pares ordenados cuyo primer componente es un elemento de A y el segundo componente es un elemento de B.
A × B = { (x,y) / x Î A ^ y Î B }
Ejemplo:
Si A = { a , b , c } y B = { 1 , 2 }
AxB = { (a,1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2) }
Note que
A tiene 3 elementos
B tiene 2 elementos
A x B tiene 6 elementos.
Producto Cartesiano
Ejemplo:
A = { corazón, trébol, coco, espada }
B = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 }
A x B = { (corazón, 1), (corazón,2),…,(corazón,12), (trébol,1), (trébol,2), …,(trébol,12), …,
(espada,12) }
Note que
A tiene 4 elementos
B tiene 12 elementos
A x B tiene 48 elementos (todas las cartas del mazo)
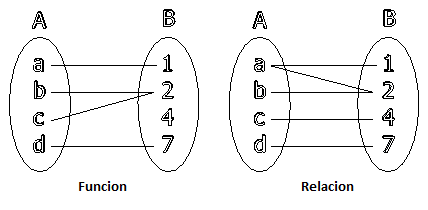
Dos conjuntos relacionados
•En una relación binaria intervienen dos conjuntos, el primero se llama «conjunto de partida» y el segundo «conjunto de llegada».
Note que
A tiene 4 elementos
B tiene 12 elementos
A x B tiene 48 elementos (todas las cartas del mazo)
Dos conjuntos relacionados
•En una relación binaria intervienen dos conjuntos, el primero se llama «conjunto de partida» y el segundo «conjunto de llegada».
Se los puede representar de las 3 formas siguientes:
Por diagrama de VENN

Producto cartesiano

Tabla de doble entrada

Producto cartesiano

Comentarios
Publicar un comentario