Ir al contenido principal

ECUACIÓN

Resultado de imagen para ecuacion animada
Ecuación
Una ecuación es una igualdad matemática entre dos expresiones, denominadas miembros y separadas por el signo igualdad, en las que aparecen elementos conocidos o datos, desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficiente o constantes; también variables o incluso objetos complejos como funciones o vectores, los elementos desconocidos pueden ser establecidos mediante otras ecuaciones de un sistema, o algún otro procedimiento de resolución de ecuaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar (en ecuaciones complejas en lugar de valores numéricos podría tratarse de elementos de un cierto conjunto abstracto, como sucede en las ecuaciones diferentes). Por ejemplo, en la ecuación algebraica simple:

Imagen relacionada
Igualdad

Es aquella que se compone de dos expresiones numéricas unidas por el signo igual.

Ejemplo:

20 + 5 = 10 + 5 + 5 + 5
1º miembro 2º miembro
Ecuación
Es aquella que contiene en sus miembros letras (incognitas) y números relacionados por operaciones aritméticas. También se puede llamar igualdad algebraica.

Ejemplo:

x+10=20-12

Propiedad Multiplicativa

Asegura que al multiplicar una misma cantidad en ambos lados, excepto 0, se obtiene el mismo resultado.

Si a = b entonces a . c = b . c

Ejemplo:

Dada la Ecuación 2x + 5 = 11

2x + 5 – 5 = 11 – 5

2x + 0 = 6

2x = 6

2 2

x = 3

Propiedad simétrica

Consiste en poder cambiar el orden de los miembros sin que la igualdad se altere.

Si a - b = c, entonces c = a - b

Ejemplos:

Si 5-1 = x entonces x = 5-1

Pasos para resolver ecuación de primer grado

3x+4=(2x+8)-(6+x)

1.Quitar paréntesis:

3x+4=2x+8-6-x

2.Pasar la incógnita al 1º miembro:

3x-2x+x=8-6-4

3.Reducir términos semejantes:

2x=-2

4.Despejar la incógnita:

x=-1

Problemas literales de Ecuaciones
Dentro de cinco años, Ximena tendrá no menos de 18 años. ¿Qué edad tiene actualmente Ximena?

Tenemos entonces:

x edad de Ximena

x + 5 edad de Ximena en 5 años

Sabemos que la edad de Ximena en cinco años será mayor que 18 años ( Dentro de cinco años, Ximena tendrá no menos de 18 años ).

x + 5 > 18

Resolvemos la inecuación:

x + 5 > 18

x > 18 -5

x > 13

Entonces podemos afirmar que Ximena actualmente tiene más de 13 años, pero no podemos determinar exactamente su edad.

EJEMPLOS DE ECUACIONES

 1.

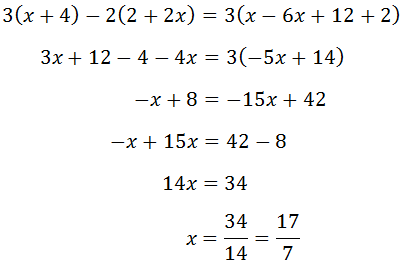
Resultado de imagen para ecuaciones
2.
Resultado de imagen para ecuaciones

Comentarios

Publicar un comentario

Entradas populares de este blog

INTERVALOS Y DESIGUALDAD

Intervalos y  Desigualdades INTERVALOS Son regiones comprendidas entre dos números reales. En general, si los extremos pertenecen al intervalo, se dice que cerrado, si por el contrario no pertenecen al intervalo, se dice que es abierto. Si uno de extremos pertenece al conjunto y el otro no, se dice que semiabierto o semicerrado. DESIGUALDAD :Es una expresión matemática que involucra los símbolos<, >, ≤, ≥.La solución de una desigualdad es el conjunto de valores que hace de la misma una expresión verdadera. La solución de una desigualdad se puede expresar en forma de intervalo, conjunto y gráfica CLASES DE INTERVALOS Intervalo abierto , (a, b), es el conjunto de todos los números reales mayores que ay menores que b. (a, b) = {x/a Es decir no incluye los extremos Intervalo cerrado, [a, b], es el conjunto de todos los números reales mayores o iguales que a y menores o iguales que b. [a, b] = {x / a ≤ x ≤ b} Incluye los extremo...
Publicar un comentario
Leer más

CONJUNTOS

CONJUNTOS DEFINICIÓN :  Colección, reunión o agrupación de objetos que poseen una característica o propiedad común bien definida. Los objetos que constituyen un conjunto se les llama miembros o elementos del conjunto NOTACIÓN Todo conjunto se escribe entre llaves { } Se denota mediante letras mayúscula.  Sus elementos se separan mediante coma. Ejemplo: El conjunto letras del alfabeto; a, b, c, ..., x, y, z. se puede escribir así: C = { a, b, c, ... x, y, z} Ejemplo: La figura adjunta es un Conjunto de Personas A = { 1, 3, 5, 7} B = {x/x2 -3x –2= 0} C = {Inglaterra, Francia, Dinamarca} RELACIÓN DE PERTENENCIA Sirve para indicar si un elemento pertenece o no a un conjunto. El símbolo de pertenencia es Є. Su negación es C = { a, b, c, ... x, y, z} b Є C (se lee: b pertenece a C) 4 C (se lee: 4 no pertenece a C) DETERMINACIÓN DE UN CONJUNTO Las formas de determinar un conjunto son: Por Extensión y Por Comprensión Diag...
Publicar un comentario
Leer más

RELACIÓN Y FUNCIÓN

Relación y Función  Producto Cartesiano El producto cartesiano de dos conjuntos A y B, denotado A × B, es el conjunto de todos los posibles pares ordenados cuyo primer componente es un elemento de A y el segundo componente es un elemento de B. A × B = { (x,y) / x Î A ^ y Î B } Ejemplo: Si A = { a , b , c } y B = { 1 , 2 } AxB = { (a,1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2) } Note que A tiene 3 elementos B tiene 2 elementos A x B tiene 6 elementos. Producto Cartesiano Ejemplo: A = { corazón, trébol, coco, espada } B = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 } A x B = { (corazón, 1), (corazón,2),…,(corazón,12), (trébol,1), (trébol,2), …,(trébol,12), …, (espada,12) } Note que A tiene 4 elementos B tiene 12 elementos A x B tiene 48 elementos (todas las cartas del mazo) Dos conjuntos relacionados •En una relación binaria intervienen dos conjuntos, el primero se llama «conjunto de partida» y el se...
Publicar un comentario
Leer más