Número reales
En matemáticas, el conjunto de los números reales (denotado por ℝ) incluye tanto a los números irracionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes
Se representan con la letra 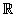 .
.
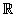 .
.
El conjunto de los Números Reales ( 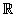 ) está integrado por:
) está integrado por:
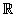 ) está integrado por:
) está integrado por:
• El conjunto de los Números Racionales (  ) que corresponden a la unión de todos los números cuya expresión decimal es finita, infinita periódica o infinita semiperiódica.
) que corresponden a la unión de todos los números cuya expresión decimal es finita, infinita periódica o infinita semiperiódica.
 ) que corresponden a la unión de todos los números cuya expresión decimal es finita, infinita periódica o infinita semiperiódica.
) que corresponden a la unión de todos los números cuya expresión decimal es finita, infinita periódica o infinita semiperiódica.
• El conjunto de los números enteros , positivos y negativos, más el cero
• El conjunto de los Números Irracionales (I) que está formado por la unión de todos los números que admiten una expresión infinita no periódica.
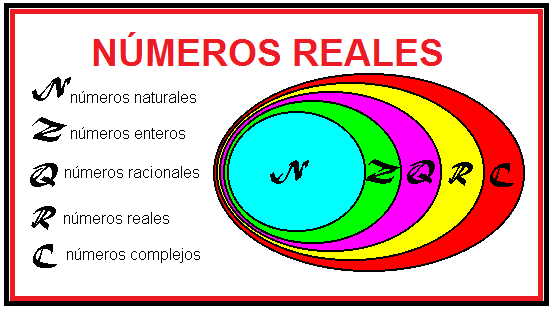
Tipos de números reales
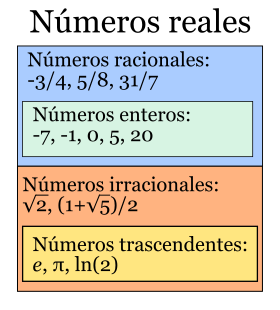
Números reales
son el conjunto de números sobre los que estudian las matemáticas, ya que son todos los números que pueden ser representados en una recta numérica. Como conjunto, los números reales contiene a los siguientes subconjuntos:
Los números enteros (Z)
que a su vez está compuesto por:
- Los números naturales (N): Son todos los números enteros positivos.
- Los números negativos.
- El cero.
Los números racionales (Q)
que son todos los que se representan por un cociente o fracción, o por números decimales exactos o periódicos. Se dividen en:
- Las fracciones, que expresan el cociente entre dos cantidades.
- Los decimales, que expresan el resultado de un cociente fraccionario.
Los números irracionales (I)
son los que expresan resultados numéricos cuyo resultado decimal no es periódico y se extiende al infinito.
Los números Trascendentes (T)
son un subconjunto de los números irracionales y algunos racionales, que expresan relaciones matemáticas muy importantes, como la relación entre la circunferencia y el radio, el número pi (π).
Generalmente el conjunto de los números reales es representado por la letra “R”, y se les aplican las operaciones y las diferentes propiedades de operación estudiadas en aritmética y en álgebra:
Comentarios
Publicar un comentario